Bachelor Thesis/Research Project/Master Thesis — Molecular Communications Channel Modeling in Capillaries
Background:
Understanding how signaling molecules move through the human microvasculature is crucial for future biomedical applications of molecular communication (MC), including early cancer detection, targeted drug delivery, and continuous health monitoring. While existing MC channel models primarily describe transport in large and medium-sized blood vessels, many envisioned applications ultimately rely on molecule exchange within the microvasculature, especially in capillaries with diameters of only 3–7 µm.
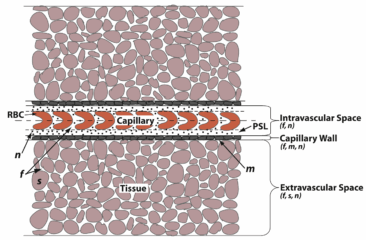
At this microscopic scale, blood behaves fundamentally differently from the macroscopic regime: red blood cells (RBCs) align in single file, flow becomes non-pulsatile and slow, and vessel walls are highly permeable. Signaling molecules distribute within plasma between RBCs, in the plasma skimming layer near the wall, and across the vessel boundary into surrounding tissue. These unique transport dynamics require dedicated models that go beyond traditional approaches used in larger vessels.
Historically, molecule transport in capillaries has been, and still is, studied extensively in medicine through models such as the Krogh tissue cylinder and more advanced mixture-theory frameworks. However, these models are often too complex to be directly applied in MC research. This project aims to close this gap by developing a simplified, MC-centric channel model for a single capillary based on established physiological modeling techniques.
Project Objectives:
- Review literature on existing mathematical models for blood flow and molecule transport in capillaries and surrounding tissue.
- Implement a simple model for a single capillary from literature as a baseline.
- Derive a new simplified model for molecule transport in a single capillary and surrounding tissue, suitable for MC.
- Compare the predictions of the derived model to predictions from existing models and optionally clinical data.
Prerequisites:
- Affinity for mathematical modeling
- Basic understanding of partial differential equations
- Basic programming skills in Python
A full description of the project can be found here. Depending on the type of project (Bachelor Thesis/Research Project/Master Thesis), the scope can be adjusted. In case you are interested in pursuing this project, please contact Timo Jakumeit (timo.jakumeit@fau.de) or Dr.-Ing. Maximilian Schäfer (max.schaefer@fau.de).